Number Systems

Number Systems 

 Introduction to Number Systems
        A number system defines a set of values used to represent quantities. In digital electronics, number systems are essential for designing and analyzing circuits.

Types of Number Systems

– Decimal System (Base-10):
– Uses digits: 0, 1, 2, 3, …, 9.
– Base = 10.
– Each digit has a place value:  10^n .

– Binary System (Base-2):
– Uses digits: 0, 1.
– Base = 2.
– Each digit has a place value:  2^n .
– Commonly used in digital electronics.

– Octal System (Base-8):
– Uses digits: 0, 1, 2, …, 7.
– Base = 8.
– Each digit has a place value:  8^n .

– Hexadecimal System (Base-16):
– Uses digits: 0–9 and letters: A, B, C, D, E, F (representing 10–15).
– Base = 16.
– Each digit has a place value:  16^n .

Conversions Between Number Systems

Decimal to Binary:

– Divide the number by 2.
– Write the remainder.
– Continue until the quotient is 0.
– Reverse the remainders.

Example:

Binary to Decimal:

– Multiply each bit by  2^n , where  n  is the bit’s position from the right  (starting at 0).
– Add the results.

Example :

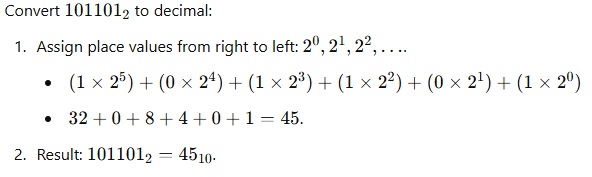
Decimal to Octal:

– Divide the number by 8 and note the remainders.
– Reverse the remainders.
Example :

Octal to Decimal:

– Multiply each bit by  8^n , where  n  is the bit’s position from the right    (starting at 0).
– Add the results.

Example :

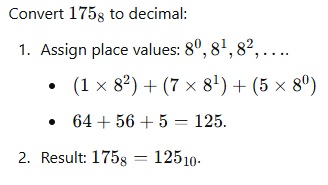
Decimal to Hexadecimal:

– Divide the number by 16 and note the remainders.
– Convert remainders above 9 to their hexadecimal equivalent.
– Reverse the remainders.

Example :

Hexadecimal to Decimal: 

– Multiply each bit by  16^n , where  n  is the bit’s position from the right             (starting at 0).
– Add the results.

Example :

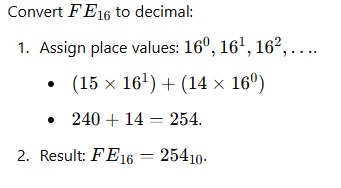
Binary to Octal:

– Group binary digits into sets of 3 (starting from the right).
– Convert each group to its octal equivalent.

Example :

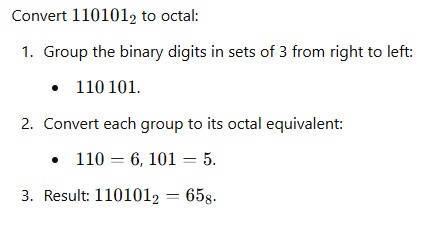
Binary to Hexadecimal:

– Group binary digits into sets of 4 (starting from the right).
– Convert each group to its hexadecimal equivalent.
Example :

 

Arithmetic Operations in Number Systems

Binary Addition:

– Follows these rules:
–  0 + 0 = 0
–  0 + 1 = 1
–  1 + 1 = 10  (carry 1)
–  1 + 1 + 1 = 11  (carry 1)
– Example:  1011 + 1101 = 11000 .

Binary Subtraction:

– Use the borrow method.
– Rules:
–  0 – 0 = 0
–  1 – 0 = 1
–  1 – 1 = 0
–  0 – 1 = 1  (borrow 1 from the next higher bit).

Binary Multiplication:

– Follows these rules:
–  0 * 0 = 0
–  0 * 1 = 0
–  1 * 1 = 1
– Example:  101 * 11 = 1111 .

Binary Division:

– Similar to decimal long division but using binary numbers.

Applications of Number Systems

Binary systems are used in:

– Digital circuits and systems.
– Microprocessors and microcontrollers.
– Data encoding and storage.
– Network communication protocols.